 |
| H Μυστηριώδης Σχέση
Ενισχυτή – Ηχείου |
Εισαγωγή
Ένα απλό μοντέλο: Κέρδος, Αντιστάσεις,
Τάσεις και Ρεύματα
Σύνθετη Αντίσταση: Πιο σύνθετη από όσο
νομίζετε...
Πηγές
Τάσης, Συντελεστής Απόσβεσης, Απόδοση και Ευαισθησία |
|
|
| Πηγές Τάσης,
Συντελεστής Απόσβεσης, Απόδοση και Ευαισθησία |
| Μια πηγή τάσης είναι,
κατά την θεωρία, μια ιδεατή πηγή η οποία μπορεί να διατηρήσει
σταθερή την τάση εξόδου της (την οποία έχουμε
επιλέξει εμείς) ανεξαρτήτως του φορτίου της. Αυτό σημαίνει ότι αν
έχουμε μια πηγή τάσης 100V και συνδέσουμε ένα φορτίο 10Ω, η πηγή μας
αποδίδει ρεύμα 10Α, αν το φορτίο γίνει 5Ω, αποδίδει 20Α, στα 2Ω το
ρεύμα φτάνει 50Α και στο 1Ω τα 100Α. Αν εξασφαλίσουμε το αδύνατον,
δηλαδή το μη καταστραφεί η πηγή από την θερμότητα των 100Α που την
διαρρέουν, και αυτό στην θεωρία γίνεται, τότε το μόνο πράγμα που
βρίσκεται ανάμεσα στην θεωρητική πηγή τάσης και σε μια
όχι-και-τόσο-καλή πηγή τάσης είναι ένα μέγεθος που
ονομάζεται εσωτερική αντίσταση. Η εσωτερική
αντίσταση της πηγής διαρρέεται από το ρεύμα του φορτίου και όσο
μεγαλύτερη είναι, τόσο υψηλότερη πτώση τάσης προκαλεί με βάση τον
νόμο του Ωμ (V=IxR). Αν η πηγή του παραδείγματος έχει εσωτερική
αντίσταση 1Ω, τότε το σύνολο του φορτίου είναι πλέον 10+1=11Ω, το
ρεύμα που αποδίδεται 100/11=9.1Α, η πτώση τάσης στην εσωτερική
αντίσταση είναι 9.1x1=9.1V και η τάση στα άκρα του φορτίου είναι
100-9.1=90.9V. Η πηγή μας δεν είναι, επομένως, μια ιδανική πηγή
τάσης (και φυσικά οι ιδανικές πηγές τάσης είναι θεωρητικό
κατασκεύασμα). Αυτός είναι ένας λόγος που θέλουμε ένα στάδιο ισχύος
να έχει πολύ χαμηλή εσωτερική αντίσταση (υπάρχουν
και άλλοι, που θα τους δούμε στη συνέχεια). Σε σχέση με το
χονδροειδές παράδειγμα μας, ένας πραγματικός ημιαγωγικός τελικός
ενισχυτής μπορεί να έχει εσωτερική αντίσταση (αντίσταση εξόδου)
μεταξύ 0.01 και 0.04Ω. Τα λαμπάτα στάδια εξόδου είναι πολύ χειρότερα
στο σημείο αυτό: κυμαίνονται μεταξύ 0.7 και 3.3Ω, είναι δηλαδή 70-80
φορές χειρότερα ως πηγές τάσης και αυτό δεν είναι άποψη, αλλά
θεωρία. |
| Πέραν της πολύ καλής
επίδοσης σε θέματα ρεύματος, η χαμηλή αντίσταση εξόδου ενός ενισχυτή
μας ενδιαφέρει και για έναν άλλο λόγο. Τον σωστό έλεγχο του ηχείου,
μια εξόχως γενική και ενίοτε κακοποιημένη έννοια η οποία σχετίζεται
με ένα μέγεθος που ονομάζεται συντελεστής
απόσβεσης. Στην πραγματικότητα, όταν λέμε “έλεγχο του
ηχείου” αναφερόμαστε στην γρήγορη απόσβεση των ταλαντώσεων ενός
κώνου όταν πάψει αυτός να ενεργοποιήται από σήμα (ή όταν το σήμα
αλλάξει πολύ σε συχνότητα και πλάτος, κάτι που είναι σχεδόν το
ίδιο). Επειδή ο κώνος ενός μεγαφώνου έχει μάζα και αναρτάται
ελαστικά, έχει και αδράνεια δηλαδή την τάση να συνεχίσει να διατηρεί
την κίνησή του ακόμη και όταν εμείς αλλάξουμε το αρχικό σήμα. Η
κίνησή του αυτή παράγει μια τάση στην είσοδο του ηχείου, με άλλα
λόγια το μεγάφωνο λειτουργεί στιγμιαία ως
γεννήτρια. Ο καλύτερος τρόπος να αποσβέσουμε την κίνηση που
έχει μορφή ταλαντώσεων με κάποια απόσβεση, είναι η εφαρμογή της
αρχής της ηλεκτρομαγνητικής πέδης όπου ένας κινητήρας, ο οποίος λόγω
αδράνειας λειτουργεί ως γεννήτρια, “φρενάρει” επάνω σε ένα βαρύ
φορτίο το οποίο τραβά πολύ ρεύμα. Το φορτίο εν προκειμένω είναι ό,τι
βλέπει το ηχείο από την είσοδό του, δηλαδή η αντίσταση εξόδου του
ενισχυτή. Όσο μικρότερη είναι αυτή τόσο ισχυρότερη η πέδη μας και
τόσο καλύτερη η απόσβεση. Ο συντελεστής απόσβεσης είναι, ακριβώς, ο
λόγος της τυπικής τιμής των 8Ω προς την αντίσταση εξόδου του
ενισχυτή. Για έναν ενισχυτή με αντίσταση εξόδου 0.01Ω ο λόγος αυτός
είναι 800. Φυσικά, υπάρχουν κι εδώ προβλήματα. Το κύκλωμα μας από
τον ενισχυτή στο ηχείο περιλαμβάνει, εκτός της αντίστασης εξόδου του
ενισχυτή τις ωμικές αντιστάσεις όλων των εξαρτημάτων του κροσόβερ
(και κυρίως των πηνίων του), την ωμική αντίσταση των πηνίων φωνής
των μεγαφώνων καθώς και τις ωμικές αντιστάσεις των καλωδίων
σύνδεσης. Μερικοί υπολογισμοί θα μας δείξουν ότι η κατάσταση
δεν είναι καθόλου αμελητέα: Χρησιμοποιώντας καλώδια ηχείων
από χαλκό με διάμετρο 1.8mm (αντίσταση 0.025Ω/m/κλάδο, Rcab) και
μήκος 3m προσθέτουμε στην αντίσταση εξόδου του ενισχυτή
3x0.05=0.15Ω, ένα πηνίο στο δρόμο του σήματος προσθέτει 0.5Ω και μια
λογική τιμή για τα πηνία φωνής είναι 6Ω. Επομένως, ο συντελεστής
απόσβεσης υπολογισμένος στον πραγματικό κόσμο θα είναι
8/(0.01+0.15+0.5+6)=1.20, ένα αποτέλεσμα καθόλου
ικανοποιητικό με βάση το ότι σύμφωνα με την βιβλιογραφία ο
συντελεστής απόσβεσης θα πρέπει να είναι μεγαλύτερος από 20.
Επομένως, το να ισχυρίζεται ένας κατασκευαστής ενισχυτών ότι το
προϊόν του έχει συντελεστή απόσβεσης 1000 δεν σημαίνει τίποτε
περισσότερο παρά το ότι έχει πολύ χαμηλή αντίσταση εξόδου.
Είναι οι αντιστάσεις που ακολουθούν τον ενισχυτή
(και ιδίως αυτές που βρίσκονται στο εσωτερικό του ηχείου) ο
καθοριστικός παράγοντας και όχι ο ίδιος ο ενισχυτής! |
 |
 |
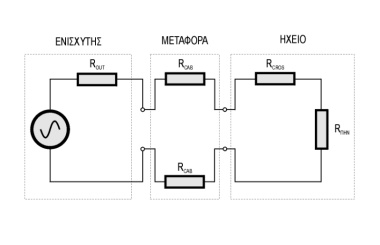
| Ένα μοντέλο μεταφοράς του σήματος από τον ενισχυτή στο
ηχείο, όπου το στάδιο ισχύος προσδιορίζεται ως πηγή σταθερής
τάσης (με εσωτερική αντίσταση Rout), τα καλώδια σύνδεσης
αντιστοιχίζονται με τις αντιστάσεις των κλάδων τους (Rcab) και
το ηχείο περιλαμβάνει μια αντίσταση που αφορά στο φίλτρο
(Rcros) και μια αντίσταση που αφορά στα πηνία φωνής
(Rπην). | |
| Τέλος, η αντίσταση
εξόδου του ενισχυτή παίζει ρόλο και σε μια ακόμη παράμετρο
λειτουργίας του συστήματος, αυτήν της επίδρασης της
μεταβολής της αντίστασης στην απόκριση συχνότητας. Ας δούμε
πως γίνεται αυτό: Ας ονομάζουμε R1 την συνολική αντίσταση του
κυκλώματος από τον ενισχυτή μέχρι την είσοδο του ηχείου και R2 την
αντίσταση του ίδιου του ηχείου. Η R1 (το άθροισμα της αντίστασης
εξόδου του ενισχυτή και της αντίστασης του καλωδίου) σχηματίζει με
την R2 ένα δικτύωμα που ονομάζεται “διαιρέτης τάσης”. Η έξοδος του
δικτυώματος αυτού (ας την πούμε Vout) είναι η τάση που εφαρμόζεται
στο ηχείο ενώ η είσοδος του (ας την πούμε Vin) η τάση εξόδου του
ενισχυτή. Ανάμεσα στην είσοδο και την έξοδο του διαιρέτη τάσης
υπάρχει η εξής σχέση: Vout=Vin x R2/(R1+R2). Επειδή γνωρίζουμε ότι η
R2 μεταβάλλεται, η σχέση αυτή είναι ανησυχητική: Δείχνει ότι
η τάση που εφαρμόζεται στο ηχείο εξαρτάται από την
διακύμανση της R2, έχουμε δηλαδή μια πηγή προβλημάτων στην
απόκριση συχνότητας εκεί που δεν το περιμέναμε! Ο μόνος τρόπος να
εξασφαλίσουμε ότι δεν θα υπάρχει διακύμανση της τάσης είναι να
αφήσουμε την R2 “μόνη” της στο κλάσμα, μηδενίζοντας την R1. Και
επειδή η R1 αποτελείται από την αντίσταση εξόδου του ενισχυτή και
την αντίσταση των καλωδίων σύνδεσης, τα καλώδια και η
αντίστασή τους μπορεί να παίξουν πολύ άσχημο παιχνίδι στο
σύστημά μας (η αντίσταση εξόδου του ενισχυτή είναι πολύ μικρή). Το
επιμύθιο; Διαλέξτε ό,τι καλώδιο θέλετε, αλλά διαλέξτε κάτι με πολύ
χαμηλή ωμική αντίσταση (δηλαδή με μεγάλη διατομή)! |
Φτάνοντας στο τέλος
του δρόμου, είναι ίσως ενδιαφέρον να δούμε τι συμβαίνει και με το
ίδιο το ηχείο. Αυτό είναι μία ηλεκτρική μηχανή και όταν έχουμε να
κάνουμε με μια ηλεκτρική μηχανή ένα από τα πράγματα που μας
ενδιαφέρουν είναι ο συντελεστής απόδοσης. Ο
συντελεστής απόδοσης είναι το πηλίκο της ισχύος που αποδίδει η
μηχανή μας προς την ισχύ που προσλαμβάνει. Επειδή πρόκειται για λόγο
μεγεθών που μετρώνται με την ίδια μονάδα (Watt) είναι αδιάστατος και
συνήθως εκφράζεται ως ποσοστό. Ο συντελεστής απόδοσης μας ενδιαφέρει
και στα ηχεία φυσικά, αλλά υπάρχει ένα σοβαρό πρόβλημα: Η μέτρηση
της ακουστικής ισχύος απαιτεί από την πλευρά μας γνώση της
ακουστικής εμπέδησης, της "αντίστασης" δηλαδή που βλέπει το ηχείο
όταν ακτινοβολεί σε έναν χώρο. Αυτή η εμπέδηση όχι μόνο δεν είναι
γνωστή, συνήθως, επειδή εξαρτάται από τις ιδιότητες του χώρου και
την θέση του ηχείου σε αυτόν, αλλά εξαρτάται και από την
κατευθυντικότητα του ίδιου του ηχείου.
Επομένως, είναι
καταρχήν δύσκολο να μετρήσουμε τον συντελεστή απόδοσης και
αν τον μετρήσουμε δεν σημαίνει και πολλά πράγματα σε έναν άλλο χώρο.
Είμαστε, λοιπόν, υποχρεωμένοι να εφεύρουμε μια μέτρηση ευκολότερη
και πιο χρήσιμη. Αυτή είναι η ευαισθησία.
Η ευαισθησία
ενός ηχείου είναι ένα αυθαίρετο μέγεθος το οποίο
χρησιμοποιήται για να μπορέσουμε να κάνουμε υπολογισμούς σε μια
ηχητική εγκατάσταση. Αυτό που συνήθως θέλουμε είναι να μάθουμε αν
ένα συγκεκριμένο ηχείο οδηγούμενο από έναν συγκεκριμένο ενισχυτή θα
μπορέσει να δημιουργήσει μια ζητούμενη στάθμη σε μια συγκεκριμένη
απόσταση. Επειδή οι ηχητικές εγκαταστάσεις σχεδιάζονται με βάση τις
ανάγκες (και όχι τις συζύγους) θεωρούμε (αυθαιρέτως, επίσης) ότι τα
ηχεία κοιτούν τους ακροατές επομένως αυτοί βρίσκονται "στον άξονα".
Επίσης, όταν επιλέγουμε έναν ενισχυτή τον πληρώνουμε "με το βατ" και
όταν μετράμε την στάθμη χρησιμοποιούμε ένα ντεσιμπελόμετρο, επομένως
το αυθαίρετο μέγεθός μας θα πρέπει να συνδέει "βατ με dBSPL και
απόσταση, στον άξονα". Έτσι προέκυψε η γνωστή έκφραση:
dBSPL/w/m. Τυπικά, τώρα, η μέτρηση της ευαισθησίας
γίνεται στην μεσαία περιοχή και αποτελεί έναν μέσο όρο ενός αριθμού
μετρήσεων. Θεωρώντας ότι στην περιοχή αυτή η τυπική εμπέδηση ενός
ηχείου είναι, υποτίθεται, 8Ω μπορούμε να εκφράσουμε την ευαισθησία
με αναφορά σε τάση και όχι σε ισχύ. Αν επί μιας αντίστασης 8Ω
εφαρμόσουμε μια τάση 2.83Vrms η ισχύς που καταναλώνεται (επομένως
και αποδίδεται από τον ενισχυτή) είναι 1W. Κάποια στιγμή,
αναπόφευκτα, η έκφραση της ευαισθησίας απέκτησε εναλλακτική μορφή,
dBSPL/2.83Vrms/m και νέο όνομα, ευαισθησία τάσης
(voltage sensitivity). |
 |
 |
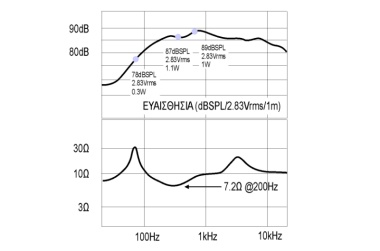
| Όταν η μέτρηση της ευαισθησίας γίνεται με αναφορά μια
τάση επί μιας αντίστασης (εδώ 2.83V/8Ω) το αποτέλεσμα δεν
μπορεί να εκφραστεί υπό σταθερή ισχύ, επειδή -στην πράξη- η
αντίσταση του ηχείου
μεταβάλλεται. | |
| Προφανώς, ένα ηχείο 4Ω
μετρημένο με τάση αναφοράς τα 2.83V, απορροφά ισχύ 2W. Eπομένως, η
ευαισθησία του μετρημένη με αυτή τη μέθοδο εμφανίζεται ως υψηλότερη
έναντι ενός 8Ωμου. Από την στιγμή που γνωρίζουμε την εμπέδηση, δεν
υπάρχει πραγματικό πρόβλημα: Απλώς αφαιρούνται 3dB
και καταλήγουμε σε αποτέλεσμα άμεσα συγκρίσιμο. Δεν υπάρχει
αμφιβολία, ότι πολλοί κατασκευαστές που χρησιμοποιούν την
προδιαγραφή "2.83V" το κάνουν εκ του πονηρού. Πριμοδοτούν το ηχείο
τους κατά 3dB (αν είναι τετράωμο). Στην πράξη βεβαίως, γνωρίζουμε
ότι η αντίσταση του ηχείου μεταβάλλεται συνεχώς σε συνάρτηση με την
συχνότητα επομένως, ούτως ή άλλως τα 2.83V (ή οποιαδήποτε άλλη τιμή)
δεν αντιστοιχεί συνεχώς στην ίδια ισχύ. Ένα ηχείο με αντίσταση 8Ω
στα 800Hz έχει ευαισθησία 89dBSPL/2.83V/m και πράγματι αναφερόμαστε
στο 1W, αλλά το ίδιο ηχείο, στα 200Hz έχει πέσει στα 7.2Ω επομένως η
ισχύς που καταναλώνει στα 2.83Vrms είναι 1.1W και η ευαισθησία του
έχει πέσει στα 87dBSPL/2.83V/m, ενώ ακόμη χαμηλότερα, στα 60Hz όπου
η αντίσταση κορυφώνεται στα 30Ω αποδίδει 78dBSPL/2.83V/m αλλά
καταναλώνει ισχύ 0.3W. Οι μετρήσεις της ευαισθησίας είναι λογικές
(το ηχείο είναι μικρό και “κόβει” γρήγορα στις χαμηλές συχνότητες)
αλλά δεν πρέπει να έχουμε την ψευδαίσθηση ότι όλες οι μετρήσεις
έχουν γίνει στο 1W. Στην πραγματικότητα, αυτό δεν μας
ενδιαφέρει και πολύ, όσο ο ενισχυτής μας προσεγγίζει τις
ιδιότητες της πηγής τάσης, επομένως μπορεί να τροφοδοτήσει επαρκώς
το φορτίο του με ρεύμα ακόμη και όταν η αντίσταση πέσει.
Επιπροσθέτως, με δεδομένο ότι η μικρότερη αντίσταση τείνει να
αυξήσει την ευαισθησία (επειδή “κρύβει” το ότι παρέχουμε περισσότερα
βατ) μπορούμε, πάντα, να χρησιμοποιήσουμε ως αναφορά όχι “ξερά” τα
2.83V αλλά την τάση που αντιστοιχεί στην πραγματική τυπική αντίσταση
του ηχείου μας η οποία είναι, εξ' ορισμού, μόλις 15% υψηλότερη της
ελάχιστης. Οι αποκλίσεις τότε θα είναι μικρές. |
Επί του
πρακτέου, τώρα, την ευαισθησία την χρειαζόμαστε σε δύο
περιπτώσεις: Στην σύγκριση δύο ηχείων (για να δούμε πιο είναι
περισσότερο ευαίσθητο) και στον έλεγχο στάθμης (για να δούμε αν ένας
συγκεκριμένος συνδυασμός ενισχυτή-ηχείου μπορεί να αποδώσει τα
δέοντα SPL).
Όταν συγκρίνουμε ηχεία, εννοείται
ότι οι συγκρίσεις θα πρέπει να γίνονται μόνο μεταξύ ομοειδών
μεγεθών: dBSPL/W/m με dBSPL/W/m και dBSPL/2.83Vrms/m με
dBSPL/2.83Vrms/m. Στην δεύτερη περίπτωση οι τυπικές αντιστάσεις
πρέπει να είναι ίδιες. Αν όχι, αφαιρούμε 3dB από το 4Ω. Δεν
ασχολούμαστε με την διακύμανση της εμπέδησης (το τάδε ηχείο "πέφτει"
στα 3Ω, κ.λπ), επειδή η ευαισθησία έχει οριστεί ως μέση τιμή στο
midband.
Όταν ελέγχουμε τις δυνατότητες για δημιουργία
στάθμης, τέλος, επειδή αγοράζουμε βατ και όχι βόλτ, οι
υπολογισμοί γίνονται "με το βατ". Θέλουμε επομένως την ευαισθησία σε
dBSPL/W/m. Αν δίδεται σε dBSPL/2.83Vrms/m θα πρέπει να κάνουμε
αναγωγή: 2.83Vrms=1Wrms/8Ω ή 2.83Vrms=2Wrms/4Ω. |
Αναφορές
1.
Acoustics, Leo L. Beranek, Acoustical Society of America, 1993
(1954)
2. High Performance Loudspeakers, 6th Edition Martin
Colloms, Wiley, 2005
3. Sound Reproduction – Loudspeakers and
Rooms, Floyd E. Toole, Focal Press, 2008
4. Συζήτηση περί ευαισθησίας στο forum του avmentor,
http://www.avmentor.eu/forum/ |
|
| |