 |
| H Μυστηριώδης Σχέση
Ενισχυτή – Ηχείου |
Εισαγωγή
Ένα απλό μοντέλο: Κέρδος, Αντιστάσεις,
Τάσεις και Ρεύματα
Σύνθετη Αντίσταση: Πιο σύνθετη από όσο
νομίζετε...
Πηγές Τάσης, Συντελεστής Απόσβεσης,
Απόδοση και Ευαισθησία |
|
|
| Σύνθετη
Αντίσταση: Πιο σύνθετη από όσο νομίζετε... |
| Ένα ηχείο είναι από
την φύση του ένα σύνθετο ηλεκτρομηχανικό σύστημα. Το γεγονός ότι
χρειάστηκαν δεκαετίες μέχρι να παρουσιαστούν καλά μοντέλα της
συμπεριφοράς του (από τους Thiele και Small για αρχή) δείχνει το
πρόβλημά μας στο να το κατανοήσουμε με τρόπο εφαρμόσιμο. Στην πράξη,
μάλιστα, εκτός των μεγαφώνων και των μηχανικών χαρακτηριστικών της
καμπίνας έχουμε και ένα φίλτρο το οποίο προηγείται συμμετέχοντας
στην συνολική συμπεριφορά του ηχείου, όπως την βλέπει ο ενισχυτής.
Αυτό που συμβαίνει στην πραγματικότητα είναι ότι, ως φορτίο,
το ηχείο είναι μια σύνθετη αντίσταση (την οποία
συχνά ονομάζουμε και εμπέδηση, impedance). Για πολλούς, “σύνθετη
αντίσταση” είναι μια αντίσταση της οποίας η τιμή αλλάζει σε
συνάρτηση με την συχνότητα, αλλά αυτό είναι μέρος μόνο της
πραγματικότητας. Η αντίσταση του ηχείου αλλάζει, πράγματι, με την
συχνότητα όπως φαίνεται και στα διάφορα διαγράμματα που
δημοσιεύονται κατά καιρούς αλλά για να καταλάβουμε τι ακριβώς
συμβαίνει θα πρέπει να κάνουμε ένα βήμα ακόμη, εξετάζοντας
την χρονική σχέση τάσης και ρεύματος σε μια τέτοια
σύνθετη αντίσταση. Στις κλασικές ωμικές αντιστάσεις της θεωρίας, η
σχέση τάσης και ρεύματος είναι γραμμική, όπως προβλέπεται από τον
νόμο του Ωμ (I=V/R). Την στιγμή που αυξάνουμε την τάση στα άκρα μιας
τέτοιας αντίστασης, αυξάνεται και το ρεύμα μέσω αυτής, χωρίς
καθυστέρηση. Το προφανές αυτό γεγονός δεν συμβαίνει στις σύνθετες
αντιστάσεις όπου οι μεταβολές της τάσης αντιστοιχούν μεν σε
μεταβολές του ρεύματος αλλά με κάποια καθυστέρηση. Σε έναν θεωρητικό
πυκνωτή η τάση καθυστερεί να “ανέβει” ενώ αυτός
διαρρέεται από υψηλό ρεύμα (λέμε ότι το ρεύμα προηγείται κατά 90
μοίρες της τάσης) ενώ φυσικά ο κλασικός, απλός νόμος του Ωμ δεν
προβλέπει τέτοια συμπεριφορά. Αντιθέτως ένα θεωρητικό πηνίο
παρουσιάζει αδράνεια στην ροή του ρεύματος. Η τάση μπορεί να
αυξάνεται στα άκρα του αλλά το ρεύμα καθυστερεί να
ακολουθήσει (λέμε ότι το ρεύμα έπεται της τάσης κατά 90 μοίρες). Όλα
αυτά είναι, βεβαίως, θεωρητικά. Στην πράξη δεν υπάρχουν εξαρτήματα
και συστήματα που να επιδεικνύουν καθαρή επαγωγική ή χωρητική
συμπεριφορά αλλά υπάρχουν ενδιάμεσες συμπεριφορές. Το ίδιο ακριβώς
συμβαίνει και με τα ηχεία. Είναι σύνθετες αντιστάσεις των οποίων το
μέτρο (σε Ω) και η φάση μεταβάλλονται με την συχνότητα ανάμεσα σε
κάποιες τιμές. |
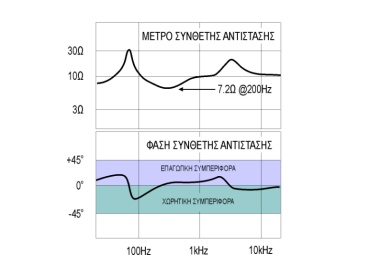
Για να περιγραφεί
πλήρως η συμπεριφορά του ηχείου ως φορτίο, επομένως, δεν
χρειαζόμαστε απλώς το διάγραμμα μεταβολής της αντίστασής του κατά
μέτρο (πόσα Ωμ είναι, δηλαδή, σε κάθε συχνότητα) αλλά και το
διάγραμμα φάσης, που δείχνει ποια είναι η διαφορά φάσης της τάσης
και του ρεύματος σε κάθε συχνότητα. Ένα τέτοιο διάγραμμα μας δείχνει
διάφορα πράγματα: Καταρχήν την ελάχιστη τιμή της αντίστασης στο
φάσμα για παράδειγμα 7.2Ω στα 200Ηz, την μέγιστη τιμή της, για
παράδειγμα 30Ω στα 60Hz καθώς και κατά πόσον το ηχείο συμπεριφέρεται
επαγωγικά (δηλαδή εισάγει καθυστέρηση στο ρεύμα) και κατά πόσον
χωρητικά (εισάγει δηλαδή προπορεία).
Σε ένα διάγραμμα
Bode (όπως ονομάζονται αυτά τα “διπλά” διαγράμματα)
παρατηρεί κανείς το εξής ανησυχητικό: Το ηχείο παρουσιάζει ωμική
συμπεριφορά σε ελάχιστες συχνότητες, ενώ σε οποιοδήποτε άλλο σημείο
του φάσματος είναι άλλοτε χωρητικό, εισάγοντας αρνητική διαφορά
φάσης μεταξύ τάσης και ρεύματος (το ρεύμα προηγείται) είτε
επαγωγικό, εισάγοντας θετική διαφορά φάσης (το ρεύμα έπεται). Ποιες
είναι οι επιπτώσεις όλων αυτών; Το μέτρο της αντίστασης μας δείχνει
πόσο ρεύμα απαιτεί το ηχείο μας σε κάθε συχνότητα από τον ενισχυτή.
Ένα χαρακτηριστικό που μας ενδιαφέρει είναι η ελάχιστη αντίσταση
επειδή αυτή καθορίζει, πρώτον, την περιοχή όπου η οδήγηση είναι
δυσκολότερη και, δεύτερον, μια τιμή αντίστασης η οποία υπολογίζεται
ως το 1.15 της ελάχιστης και ονομάζεται “τυπική αντίσταση” του
ηχείου (nominal impedance). H φάση της αντίστασης μας βοηθά να
καταλάβουμε πόσο ταλαιπωρεί θερμικά τον ενισχυτή μας το ηχείο και σε
ποια συχνότητα. |
 |
 |
| Ο
τρόπος με τον οποίο μεταβάλλεται κατά μέτρο (επάνω) και φάση
(κάτω) η αντίσταση ενός ηχείου. Μπορούμε να διακρίνουμε την
ελάχιστη τιμή αντίστασης καθώς και την συμπεριφορά της
(επαγωγική ή χωρητική) ανάλογα με την διαφορά φάσης που
εισάγει μεταξύ τάσης και
ρεύματος. | |
| Για να γίνει κατανοητό
αυτό αξίζει να επανέλθουμε στο αρχικό, απλό μοντέλο
μας όπου η τάση και το ρεύμα συμβαδίζουν. Μια στάθμη εξόδου 80V στα
100Hz (όπου η αντίσταση, σύμφωνα με το διάγραμμα είναι 10Ω) προκαλεί
ρεύμα 8Α (80/10) και η ισχύς που καταναλώνεται στο ηχείο είναι
80x8=640W (θυμίζω ότι μιλάμε για εικονικές τιμές). Η συνολική ισχύς
που αποδίδει ο ενισχυτής είναι αυτά τα 640W αθροιζόμενα με την ισχύ
θερμικών απωλειών (20V στα άκρα του ημιαγωγού με ρεύμα 8Α),
20x8=160W με το σύνολο 640W+160W=800W, αποτέλεσμα αναμενόμενο από
την στιγμή που έχουμε στα χέρια μας ένα τροφοδοτικό τάσης 100V το
οποίο αποδίδει 8A. Ωστόσο, το διάγραμμα μας δεν δείχνει απλώς ότι το
ηχείο έχει αντίσταση 8Ω, την συγκεκριμένη χρονική στιγμή, αλλά και
ότι υπάρχει μια διαφορά φάσης περίπου 20 μοιρών (χωρητική, δηλαδή η
τάση έπεται του ρεύματος). Αυτό αλλάζει τον υπολογισμό της ισχύος
επάνω στο ηχείο, εισάγοντας το περίφημο “συνημίτονο
φ”, την γωνία της διαφοράς φάσης. Τώρα, με βάση την θεωρία,
η ισχύς που αποδίδει ο ενισχυτής στο φορτίο του είναι
80x8xσυν(20)=601.4W, περίπου 40W λιγότερα από ότι αν η αντίσταση
ήταν ωμική. Το πρόβλημα, φυσικά, είναι ότι τα 40W δεν
χάνονται αλλά καταναλώνονται στο στάδιο ισχύος ως
θερμότητα, 800-601.4=198.6W, τιμή αυξημένη σε σχέση με τα 160W που
υπολογίσαμε με την ωμική αντίσταση. Το παράδειγμα είναι αρκετά
φιλικό προς τους ενισχυτές. Στην αγορά κυκλοφορούν ηχεία που
εισάγουν διαφορές φάσης ίσως και πάνω από 50 μοίρες, έχουν πολύ
χαμηλότερες ελάχιστες αντιστάσεις και, το χειρότερο, πιο συχνά από
όσο θα έπρεπε, η ελάχιστη αντίσταση μπορεί να συμπέσει με
την μεγαλύτερη διαφορά φάσης (ή να βρίσκεται στην ίδια
ευρύτερη περιοχή), φορτίζοντας τον ενισχυτή ταυτοχρόνως και με υψηλό
ρεύμα και με ένα “μικρό” συν(φ). Οι απώλειες στο στάδιο ισχύος
αυξάνονται κατακόρυφα και, συχνά, το προστατευτικό του ενισχυτή
ενεργοποιήται χωρίς προφανή αιτία (“μα δεν άκουγα πολύ δυνατά...").
|
Συνοψίζοντας, μπορούμε να πούμε τα
εξής:
Το ηχείο είναι μια σύνθετη αντίσταση με μέτρο και φάση. Το
μέτρο καθορίζει το ρεύμα που θα κληθεί να δώσει ο
ενισχυτής ενώ η φάση τις θερμικές απώλειες που
υπάρχουν στο στάδιο εξόδου. Για να χαρακτηρίσουμε ένα ηχείο ως
εύκολο ή δύσκολο φορτίο δεν αρκεί μόνο το διάγραμμα
του μέτρου της αντίστασης αλλά και το διάγραμμα της φάσης.
Τα χειρότερα φορτία είναι αυτά με χαμηλό μέτρο
αντίστασης που συμπίπτει ή βρίσκεται στην γειτονιά μεγάλων διαφορών
φάσης. Έχοντας όλα αυτά υπόψιν μας γίνεται αντιληπτό ότι αν θέλουμε
να είμαστε σίγουροι ότι ένας ενισχυτής είναι γενικής χρήσης (οδηγεί
δηλαδή τα περισσότερα ηχεία με άνεση) τότε θα είναι ένας
μεγάλος ενισχυτής, τόσο σε δυνατότητες ρεύματος όσο
και σε δυνατότητες ψύξης. Όσον αφορά τις τελευταίες το πράγμα είναι
απλό: Χρησιμοποιούνται ημιαγωγοί με μεγάλη αντοχή σε θερμότητα και
ανάλογες ψύκτρες. Όσον αφορά την οδήγηση, η θεωρία έχει έναν όρο για
τους ενισχυτές που μπορούν να οδηγήσουν “δύσκολα” φορτία. Τους
κατατάσσει στις πηγές τάσης. |
|
| |