 |
| Ακουστική Μικρών Χώρων |
Εισαγωγή – Περί Ακουστικής Μικρών
Χώρων
Τα Βασικά Χαρακτηριστικά – Χρόνος
Αντήχησης και Ηχοαπορρόφηση
Χαμηλές συχνότητες και Στάσιμα Κύματα
Υψηλές συχνότητες και Ανακλάσεις
Στην Πράξη... |
|
|
| Χαμηλές
συχνότητες και Στάσιμα Κύματα |
Αν υποθέσουμε
ότι έχουμε ένα μηχανικό σύστημα του οποίου τα δομικά μέρη συνδέονται
μεταξύ τους ελαστικά τότε για κάποια συγκεκριμένη διέγερση (και με
δεδομένα τα χαρακτηριστικά των ελαστικών συνδέσμων και τις μάζες των
μερών) το σύστημα αυτό θα εκτελέσει μια ιδιόμορφη κίνηση κατά την
οποία το κάθε μέρος του εκτελεί αρμονική ταλάντωση με την ίδια
συχνότητα. Τότε, λέμε ότι έχουμε βρει ένα ιδιορυθμό (eigenmode),
έναν φυσικό ρυθμό (normal mode) ή μια φυσική συχνότητα, ή συχνότητα
συντονισμού του συστήματος. Καθώς τα μέρη του συστήματος
ταλαντώνονται με την ίδια συχνότητα, βρίσκονται είτε σε φάση είτε σε
αντίθεση φάσης, κάτι το οποίο σημαίνει ότι οι ταλαντώσεις που
πραγματοποιούνται είναι οι μέγιστες δυνατές. Αν μοντελοποιήσουμε τον
αέρα που περιέχεται μέσα σε έναν χώρο ως ένα σύνολο στοιχειωδών
μαζών που συνδέονται μεταξύ τους ελαστικά, τότε έχουμε στα χέρια μας
ένα πολύπλοκο μηχανικό σύστημα τριών διαστάσεων το οποίο θα
παρουσιάζει ιδιορυθμούς.
Από θεωρητικής πλευράς, οι ιδιορυθμοί
εμφανίζονται ως οι λύσεις συστημάτων διαφορικών εξισώσεων με την
χρήση πινάκων και χαρακτηρίζουν την συμπεριφορά (δηλαδή την γενική
λύση) του συστήματος. Οι ιδιορυθμοί ενός χώρου στην ακουστική
ονομάζονται στάσιμα κύματα. Έχοντας ως δεδομένο έναν χώρο με
συγκεκριμένη γεωμετρία ο αριθμός των στάσιμων κυμάτων που τον
χαρακτηρίζουν είναι άπειρος, ωστόσο αυτοί που μας ενδιαφέρουν
ιδιαίτερα είναι συγκεκριμένοι. Οι ιδιορυθμοί διεγείρονται από την
ανάκλαση του ηχητικού κύματος στα όρια ενός χώρου και με το σκεπτικό
αυτό μπορούμε να διακρίνουμε τρεις κατηγορίες: Τους αξονικούς
ρυθμούς οι οποίοι διεγείρονται από δύο παράλληλους τοίχους, τους
πλάγιους ρυθμούς οι οποίοι διεγείρονται από διαδοχικές
ανακλάσεις στους τοίχους του χώρου και τους εφαπτομενικούς
ρυθμούς οι οποίοι διεγείρονται από διαδοχικές ανακλάσεις τόσο στους
τοίχους όσο και στην οροφή και στο δάπεδο του χώρου. Ταυτόχρονα,
στον βασικό ιδιορυθμό (κάθε περίπτωσης) αντιστοιχεί ένα άπειρο
πλήθος ιδιορυθμών που είναι πολλαπλάσιά του κατά την λογική των
αρμονικών. Αυτό σημαίνει ότι δεν είναι δυνατόν να υπολογίσουμε όλους
τους ιδιορυθμούς ενός χώρου, ούτε και το θέλουμε άλλωστε. Αυτοί που
μας ενδιαφέρουν είναι οι βασικοί (ή πρώτοι) ιδιορυθμοί και τα πρώτα
τους πολλαπλάσια (δεύτερος, τρίτος και τέταρτος ιδιορυθμός) και,
όσον αφορά την ακουστική μικρών και μάλιστα οικιακών χώρων, μόνον οι
αξονικοί, επειδή αυτοί είναι που σε σημαντικό ποσοστό καθορίζουν την
συμπεριφορά του χώρου στις χαμηλές συχνότητες, καθώς οι μεν
εφαπτομενικοί έχουν στάθμες 3dB και οι δε πλάγιοι 6dB
χαμηλότερα από τους αξονικούς. Πριν προχωρήσουμε στον υπολογισμό των
ιδιορυθμών θα πρέπει, ίσως, να ασχοληθούμε με την φυσική τους
υπόσταση: Είναι αρκετά δύσκολο να φανταστεί κανείς τον ιδιορυθμό ως
φυσική έννοια ακόμη και σε δύο διαστάσεις μιας χορδής, πόσο μάλλον
σε τρεις διαστάσεις του χώρου. Ρίξτε μια ματιά σε αυτή την
εφαρμογή (Java applet) η οποία είναι ένα καλό εποπτικό μέσον, αφού πρώτα διαβάσετε
το υπόλοιπο κείμενο (εδώ) και τις οδηγίες χρήσης (στον δικτυακό τόπο
της εφαρμογής) |
 |
 |
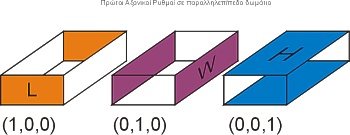
| Τα
όρια του χώρου που συμμετέχουν στην δημιουργία των τριών
πρώτων αξονικών ρυθμών. Οι παράλληλοι τοίχοι οι οποίο
χωρίζονται από την μεγαλύτερη διάσταση του χώρου είναι
υπαίτιοι για τον ρυθμό (1,0,0), οι τοίχοι που καθορίζουν το
πλάτος του χώρου για τον ρυθμό (0,1,0) και στο ζεύγος
οροφή-δάπεδο οφείλεται ο ρυθμός
(0,0,1) | |
| Στάσιμα
Κύματα: Είδη και υπολογισμοί. |
| Ο υπολογισμός
των ιδιορυθμών (δηλαδή -θυμίζω- των συχνοτήτων των στάσιμων κυμάτων
που δημιουργούνται σε έναν συγκεκριμένο χώρο) βασίζεται σε μια απλή
μαθηματική σχέση: |
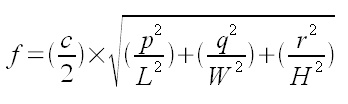 |
με το
c=340.29m/sec, τα L, W, H να αντιστοιχούν στο μήκος, το πλάτος και
το ύψος του χώρου και τα p, q, r να είναι ακέραιοι οι οποίοι
παίρνουν τιμές 0,1,2,...
Οι συνδυασμοί των p, q και r είναι
φυσικά άπειροι και αυτό εκφράζει και το απειράριθμο των ιδιορυθμών.
Ωστόσο, από τους συνδυασμούς τους μας ενδιαφέρουν
συγκεκριμένοι:
1,0,0 -το στάσιμο κύμα που δημιουργείται κατά
μήκος της μεγάλης διάστασης του χώρου
0,1,0 – το στάσιμο κύμα που
δημιουργείται κατά μήκος του πλάτους
0,0,1 – το στάσιμο κύμα που
δημιουργείται από το δάπεδο και την οροφή
καθώς και τα
πολλαπλάσιά τους (2,0,0, 3,0,0, 0,3,0 κ.λπ) τα οποία αντιστοιχούν
στους δεύτερους, τρίτους, κ.λπ τρόπους ταλάντωσης δηλαδή σε στάσιμα
κύματα διπλάσιας, τριπλάσιας κ.λπ συχνότητας. Κατ΄αναλογίαν, ο
πρώτος εφαπτομενικός ιδιορυθμός (το στάσιμο κύμα από διαδοχικές
ανακλάσεις στους τοίχους) θα είναι αυτό που αντιστοιχεί στον
συνδυασμό (1,1,0) και το πρώτο πλάγιο στάσιμο κύμα, από διαδοχικές
ανακλάσεις σε όλα τα όρια του χώρου, το (1,1,1).
Η λύση της
εξίσωσης είναι απλή: Απλώς αντικαθιστούμε τα p,q,r και L, H, W. Έτσι
για ένα δωμάτιο συμβατό με τις απαιτήσεις του IEC (διαστάσεις
7.0x5.3x2.7m) οι πρώτοι αξονικοί ρυθμοί θα είναι: 24.3Ηz, 32.1Ηz και
63Hz. |
 |
 |
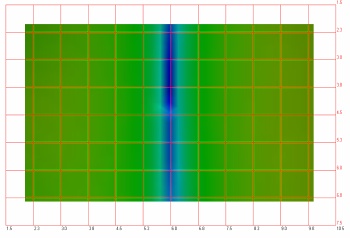
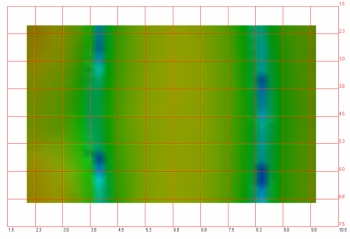
| Χρωματική κωδικοποίηση της εξέλιξης ενός ηχητικού
πεδίου σε συνάρτηση με την συχνότητα σε έναν χώρο, όπως αυτή
προβάλλεται στην κάτοψη Οι έντονες χρωματικές περιοχές
υποδηλώνουν σημεία υψηλής πίεσης ενώ οι πιο “ψυχρές” σημεία
χαμηλής πίεσης. Εδώ φαίνεται ο πρώτος αξονικός ρυθμός κατά
μήκος του χώρου... | |
| Ελέγχοντας
τους ρυθμούς: Διατάσεις και αναλογίες χώρων. |
|
Ποιά είναι η χρησιμότητα
ενός τέτοιου προσδιορισμού στάσιμων κυμάτων; Με δεδομένο ότι όπου
υπάρχουν όρια στον χώρο υπάρχουν και στάσιμα κύματα, είναι αυτονόητο
ότι δεν μπορούμε να τα καταργήσουμε, Μπορούμε όμως να επιλέξουμε
χώρους με τέτοιες διαστάσεις ώστε οι συχνότητες των στάσιμων κυμάτων
να είναι κατανεμημένες, με αρκετή απόσταση μεταξύ τους ώστε να μην
συμπίπτουν αλλά και αρκετά κοντά ώστε να μην μπορούμε να διακρίνουμε
κάποιον ως διακριτή πηγή. Σύμπτωση δύο ή περισσότερων αξονικών
ρυθμών σημαίνει μεγάλη ενίσχυση της συγκεκριμένης συχνότητας (καθώς
και γειτονικών συχνοτήτων, εδώ έχουμε να κάνουμε με ένα φαινόμενο
συντονισμού που χαρακτηρίζεται από ένα Q) και αυτό θέλουμε να το
αποφύγουμε. Ένα πρώτο βήμα είναι να μην επιλέξουμε χώρους με δύο ή
περισσότερες διαστάσεις ίδιες (δηλαδή τετράγωνους ή κυβικούς) ή και
χώρους με διαστάσεις από τις οποίες η μια είναι ακέραιο πολλαπλάσιο
της άλλης. Ενώ ένας κυβικός ή τετράγωνος είναι σπάνιος, η κατηγορία
των χώρων με πλευρές που είναι πολλαπλάσιες η μια της άλλης είναι
υπαρκτή. Για παράδειγμα, ένας χώρος με μήκος 8m και πλάτος 4m, έχει
πρώτους αξονικούς ρυθμούς 21 και 42Hz αντιστοίχως, οι οποίοι δεν μας
ενοχλούν ιδιαίτερα. Ωστόσο, ο δεύτερος αξονικούς ρυθμός που
αντιστοιχεί στο μήκος είναι κι αυτός 42Hz! Αυτό είναι ένα
πρόβλημα...
Εννοείται, ότι η απόλυτη σύμπτωση δεν είναι το μόνο
που μας ενδιαφέρει. Και η μερική σύμπτωση προκαλεί παρόμοια
προβλήματα. Στην βιβλιογραφία συναντούμε δύο διαφορετικά κριτήρια
για το θέμα αυτό: Σύμφωνα με τον Gilford, μια απόσταση μικρότερη των
20Ηz μεταξύ των στάσιμων κυμάτων θεωρείται επαρκής ώστε αυτά να μην
θεωρούνται ως πλήρως απομονωμένα με πιθανότητα να δημιουργήσουν έναν
ιδιαίτερα έντονο χρωματισμό (χωρίς να τίθεται θέμα σύμπτωσης) ενώ το
κριτήριο Bonello απαιτεί ως ελάχιστη απόσταση μεταξύ δύο γειτονικών
ρυθμών μια διαφορά 5%. |
 |
 |
| ... ο δεύτερος αξονικός ρυθμός, επίσης κατά
μήκος... | |
| Κριτήρια
Καταλληλότητας |
|
Η προφανής λύση, επομένως,
είναι να χρησιμοποιούμε χώρους με “περίεργες” αναλογίες, αλλά,
υπάρχει και η κομψή προσέγγιση των κριτηρίων καταλληλότητας. Τα
κριτήρια καταλληλότητας μας δίνουν αναλογίες χώρων που εμπειρικώς
έχουν αποδειχθεί ως καλοί. Υπάρχουν δε, αρκετά από
αυτά: |
| Κατά
τον: |
H
[m] |
W
[m] |
L[m] |
| Sepmeyer (i) |
1.00 |
1.14 |
1.39 |
| Sepmeyer (ii) |
1.00 |
1.28 |
1.54 |
| Sepmeyer (iii) |
1.00 |
1.60 |
2.33 |
| Louden (i) |
1.00 |
1.40 |
1.90 |
| Louden (ii) |
1.00 |
1.30 |
1.90 |
| Louden (iii) |
1.00 |
1.50 |
2.50 |
| Volkmannn |
1.00 |
1.50 |
2.50 |
| Bonner |
1.00 |
1.60 |
1.59 |
| Τυποποιημένα
δωμάτια: |
|
|
|
| IEC 60268 -13 |
2.70 |
5.30 |
7.00 |
| IEC 60268 -13 |
2.80 |
4.20 |
6.70 | |
 |
 |
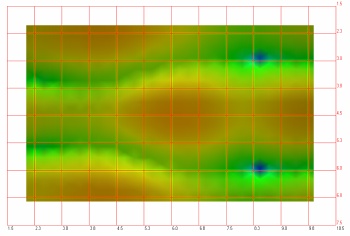
| ... ενώ εδώ μπορούμε να διακρίνουμε τον δεύτερο αξονικό
ρυθμό κατά πλάτος. Είναι προφανές ότι στις αντίστοιχες
συχνότητες δημιουργούνται χρωματισμοί, με έντονες κορυφώσεις
της πίεσης... | |
|
Μια γενίκευση
όλων των παραπάνω, είναι η λεγόμενη περιοχή Bolt ένα διάγραμμα
αναλογιών δύο διαστάσεων (πλάτους και μήκους) η οποία περιλαμβάνει
τις περισσότερες από τις “καλές” αναλογίες και το οποίο μπορεί να
βρεθεί στην βιβλιογραφία. |
 |
 |
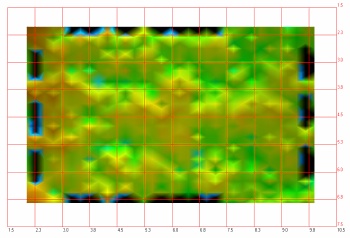
| ...αντιθέτως, όταν το δωμάτιο αποκτήσει αναλογίες
προβλεπόμενες από κάποιο κριτήριο (εδώ του IEC) η κατανομή των
ιδιορυθμών γίνεται με τέτοιο τρόπο ώστε δεν έχουμε σημαντικά
προβλήματα. Αξίζει να σημειωθεί ότι σε μια εξομοίωση η οποία
περιλαμβάνει δύο ηχεία και πραγματικές συνθήκες, τα στάσιμα
κύματα είναι, προφανώς διαφοροποιημένα σε σχέση με μια μελέτη
“στο χαρτί”. | |
| Συνοψίζοντας, είναι σημαντικό να γίνει κατανοητό το ότι τα
στάσιμα κύματα δεν είναι ένα “ατύχημα” του χώρου (δεν έχει νόημα,
δηλαδή να λέει κανείς “ο χώρος μου έχει στάσιμα κύματα”) επειδή
είναι χαρακτηριστικό γνώρισμά του, από την στιγμή που έχει τοίχους!
Ατυχές είναι είτε το γεγονός της σύμπτωσης στις συχνότητες των
στασίμων κυμάτων που οφείλονται σε διαφορετικούς ιδιορυθμούς, είτε η
ύπαρξη ενός εντελώς απομονωμένου ιδιορυθμού ο οποίος θα ακουστεί ως
χρωματισμός. Και φυσικά δεν τελειώνουμε εδώ και τόσο απλά, επειδή
αυτό που ακολουθεί είναι οι ανακλάσεις... |
|
| |