

Δικτυακός τόπος για τις Τεχνολογίες Audio, Video, HiFi, High End, Home Entertainment
Greek site for Audio Video & Home Entertainment technologies
Tελευταία Ενημερωση/Last Update: Τρίτη, 28/09/2010
Τυφλές Δοκιμές (Blind Tests): Τι είναι και πως γίνονται τελικώς;
Αν και η ανοικτή ακρόαση έχει και αυτή τους κανόνες της, τόσο όσον αφορά στην ίδια την διαδικασία όσο και στην εξαγωγή των συμπερασμάτων (κανόνες στους οποίους θα αναφερθούμε στο δεύτερο κείμενο της σειράς αυτής), αυτό που είναι πραγματικά άγνωστο στους περισσότερους ενδιαφερόμενους είναι η τυφλή δοκιμή. Αναφέρθηκε ήδη ότι μια τυφλή δοκιμή είναι μια διαδικασία όπου εξασφαλίζεται ότι οι κρίνοντες δεν γνωρίζουν τίποτε για τα αντικείμενα της κρίσης τους και περιορίζονται στην ακουστική εντύπωση. Επιπρόσθετα, μια διπλά τυφλή δοκιμή (double blind test) είναι μια τυφλή δοκιμή όπου ούτε αυτός που την πραγματοποιεί γνωρίζει το αντικείμενο, την σειρά παρουσίασης των διάφορων εκδοχών, κλπ. Την εποχή που ξεκίνησαν οι τυφλές δοκιμές αυτού του είδους οι διαδικασίες ήταν εξαιρετικά επίπονες. Φανταστείτε τι σήμαινε, τότε, να δοκιμάσεις “τυφλά” κεφαλές, για παράδειγμα, ή να ελέγξεις το πρόγραμμα που, στην καλύτερη περίπτωση προερχόταν από μαγνητικές ταινίες! Στο [3] δίνεται το κύκλωμα ενός μεταγωγού για δοκιμές A/B/X αυτής της... πρώιμης εποχής το οποίο χρησιμοποιεί μια γεννήτρια ψευδοτυχαίων γεγονότων για να να επιλέγει κάθε φορά το “X”. Όπως θα δούμε στο τελευταίο μέρος του κειμένου αυτού, σήμερα οι δυνατότητές μας είναι απείρως μεγαλύτερες.
Το απλούστερο είδος τυφλής δοκιμής είναι η σύγκριση μεταξύ δύο εκδοχών, όπου ως εκδοχές λογίζονται δύο διαφορετικές συσκευές, δύο επεξεργασίες ή δύο τεχνολογίες. Οι ακροατές καλούνται να ξεχωρίσουν τις δύο εκδοχές και, πιθανόν, να τις αξιολογήσουν. Αυτή η δοκιμή ονομάζεται “Α/Β” ή Σύγκριση Ζευγών (Pair Comparison).
Εξέλιξη της δοκιμής “A/B” είναι η Πολλαπλή Σύγκριση με Κρυμμένη Αναφορά (ABC/HR), όπου υπάρχουν περισσότερες των δύο εκδοχών και, επιπροσθέτως, μια από τις εκδοχές αυτές είναι η αναφορά της δοκιμής, συνήθως ένας διαφανής βρόχος ή μια κορυφαία συσκευή ή επεξεργασία. Ο ακροατής καλείται, καταρχήν να διακρίνει την αναφορά, βαθμολογώντας την άριστα και στη συνέχεια να διακρίνει τις άλλες εκδοχές και να τις αξιολογήσει αναλόγως.
Μια ενδιαφέρουσα, όσο και αρκετά σύνθετη περίπτωση τυφλής δοκιμής είναι το, αρκετά συζητημένο, τεστ MUSHRA (Μultiple Stimuli with Hidden Reference and Anchor). Κατά τη διαδικασία αυτή, ο ακροατής έχει στη διάθεσή του μια σειρά από εκδοχές (προς κρίση), την εκδοχή αναφοράς την οποία θα πρέπει να διακρίνει και μια ή περισσότερες εκδοχές “στήριξης”, με ποιότητα υποδεέστερη της αναφοράς έτσι ώστε να μπορεί να βαθμολογήσει με σχετική ακρίβεια και χωρίς να υπερβάλει (περισσότερες λεπτομέρειες για την αξιολόγηση με βαθμολογίες και επίθετα στο δεύτερο μέρος του κειμένου αυτού). Το MUSHRA χρησιμοποιήται σε δοκιμές όπου οι ηχητικές διαφορές αναμένεται να είναι μέτριες ή/και μεγάλες και αποτελεί την προτεινόμενη διαδικασία (από τον διεθνή οργανισμό ITU) για την αξιολόγηση codecs.
Τέλος, η δοκιμή A/B/X είναι ίσως η πιο αναλυτική και ευαίσθητη διαδικασία που έχουμε σήμερα στη διάθεσή μας, ιδιαίτερα για δοκιμές όπου οι διαφορές αναμένεται να είναι μικρές ή πολύ μικρές. Κατά την διαδικασία μιας δοκιμής A/B/X παρουσιάζονται στον ακροατή δύο εκδοχές (A και B) τις οποίες αυτός μπορεί να ακούσει όσες φορές και για όση χρονική διάρκεια επιθυμεί. Όταν ο ίδιος αποφασίσει ότι αναγνωρίζει τις δύο εκδοχές, του παρουσιάζεται μια τρίτη, η “Χ”, η οποία μπορεί να είναι είτε η Α είτε η Β, κάτι που αποφασίζεται τυχαία, είτε με κάποια μέθοδο όπως τα λατινικά τετράγωνα είτε με ηλεκτρονικό τρόπο (σήμερα). Σκοπός του είναι να αναγνωρίσει το “Χ”, μεταξύ των Α και Β. Η διαδικασία μπορεί να επαναληφθεί με πολλά διαφορετικά τρακς και σε κάθε τρακ η εκδοχή που αντιστοιχεί στο Α και στο Β αλλάζει, επίσης με τυχαίο τρόπο.
Όλες οι διαδικασίες τυφλής δοκιμής περιλαμβάνουν οπωσδήποτε ένα στάδιο αναγνώρισης όπου ο ακροατής θα πρέπει να αποδείξει ότι μπορεί να ξεχωρίσει τις δύο εκδοχές και προαιρετικά ένα στάδιο αξιολόγησης με κάποια μέθοδο. Είναι προφανές, ότι δεν υπάρχει λόγος αναλυτικής αξιολόγησης αν αποδειχθεί (με εργαλεία που θα εξετάσουμε αμέσως) ότι ο ακροατής ή το σύνολο μιας ομάδας δεν μπορεί να ανιχνεύσει διαφορές μεταξύ των εκδοχών.
Όπως κάθε διαδικασία από την οποία περιμένουμε στοιχειώδη ακρίβεια και επαναληψιμότητα, έτσι και οι τυφλές δοκιμές, ανεξαρτήτως είδους και μεγέθους, πρέπει να πληρούν κάποιες ελάχιστες προϋποθέσεις. Έτσι:
Θεωρείται αυτονόητο ότι οι στάθμες μεταξύ των εκδοχών πρέπει να είναι ρυθμισμένες με ακρίβεια και ίσες.
Το σύστημα όπως διαμορφώνεται στις διάφορες εκδοχές του (με την εισαγωγή διαφορετικών συσκευών για παράδειγμα) πρέπει να είναι αμετάβλητο. Αυτό σημαίνει ότι τα φορτία που βλέπουν οι διάφορες συσκευές, οι καλωδιώσεις και κάθε άλλη παράμετρος δεν οδηγεί σε διαφοροποιήσεις της απόκρισης συχνότητας.
Η απόλυτη φάση του συστήματος στις διάφορες εκδοχές θα πρέπει να είναι σταθερή. Αν, για παράδειγμα η μια εκδοχή αναστρέφει την φάση, σύμφωνα με την βιβλιογραφία, εισάγει πόλωση στην διαδικασία.
Η συνολική διάρκεια της δοκιμής αλλά και η επιμέρους διάρκειας των μουσικών κομματιών πρέπει να λαμβάνουν υπόψιν την κόπωση των ακροατών. Οι απόψεις ποικίλλουν, αλλά διάρκειες από 30 λεπτά μέχρι 2 ώρες θεωρούνται αποδεκτές με κάθε μουσικό κομμάτι να μην διαρκεί περισσότερο από 30 δευτερόλεπτα (ανεξαρτήτως του πόσες φορές θα το ακούσει ο κάθε ακροατής).
Η έρευνα γύρω από τις τυφλές δοκιμές έδειξε ότι οι εκπαιδευμένοι και οι έμπειροι ακροατές αποδίδουν γενικώς καλύτερα. Με τον όρο “εκπαιδευμένος” ακροατής νοείται ο ακροατής ο οποίος έχει ακούσει ηχητικά παραδείγματα και γνωρίζει για το φαινόμενο που αναζητεί και καλείται να κρίνει. Συχνά, η εκπαίδευση γίνεται με πρόγραμμα που περιλαμβάνει ισχυρά δείγματα του φαινομένου. Με τον όρο “έμπειρος” νοείται ο ακροατής που έχει ήδη μία ή περισσότερες τυφλές δοκιμές στο ενεργητικό του.
Η αξία σε μια τυφλή δοκιμή έγκειται στο ότι συνοδεύεται από μια σειρά εργαλείων που επιτρέπουν την αντικειμενική της αξιολόγηση. Έχει ήδη αναφερθεί ότι μια καλά στημένη δοκιμή αυτού του είδους βασίζεται σε μια απλή αποστολή προς τους ακροατές, με άλλα λόγια το ζητούμενο από αυτούς είναι, αρχικώς τουλάχιστον, κάτι απλό. Το πιο συνηθισμένο ερώτημα είναι “Ποια Εκδοχή Ακούτε;”, η απάντηση στο οποίο μπορεί να είναι σωστή ή λάθος, χωρίς κάποια ενδιάμεση δυνατότητα επιλογής. Μια τέτοια διαδικασία είναι γνωστή, στην στατιστική, ως δοκιμή Bernoulli, η πλέον διάσημη εκδοχή της οποίας είναι το στρίψιμο ενός νομίσματος.
Φανταστείτε ότι στρίβετε ένα νόμισμα μερικές δεκάδες φορές και καταγράφετε την πλευρά με την οποία καταλήγει σε μια επιφάνεια. Αν το νόμισμα είναι “τίμιο” δηλαδή ομοιογενές ως προς την κατανομή της μάζας, αναμένετε τα “Γράμματα” και οι “Κορώνες” να εμφανιστούν περίπου ίσες φορές. Θεωρητικά, η πιθανότητα ενός τέτοιου νομίσματος να πέσει με την μία ή την άλλη πλευρά είναι 0.50 (ή 50%) και η πιθανότητα αυτή προσεγγίζεται καθώς η επανάληψη του πειράματος τείνει προς το άπειρο. Αν στρίψετε ένα νόμισμα 100 φορές και καταλήξει στα “Γράμματα” 80 φορές, αρχίζετε να υποψιάζεστε ότι κάτι δεν πάει καλά...
Μια τυφλή δοκιμή είναι, από μαθηματικής άποψης, μια δοκιμή Bernoulli, μόνο που στην περίπτωση αυτή, αυτό που αναζητούμε είναι το αν έχουμε λόγους να πιστέψουμε ότι ο ακροατής δεν επιλέγει τυχαία, αν δηλαδή η πιθανότητα επιλογής μεταξύ του Α και του Β είναι μεγαλύτερη από 0.50. Σε μια δοκιμή όπου έχουμε περίπου ίση κατανομή σωστών και λάθος επιλογών (αυτό σημαίνει ότι οι σωστές επιλογές έχουν πιθανότητα 0.50 να εμφανιστούν) δικαιούμεθα να θεωρήσουμε ότι ο ακροατής (ή η ομάδα) μη μπορώντας να ξεχωρίσει τις εκδοχές, απλώς μαντεύει στην τύχη. Αν πιθανότητα είναι μεγαλύτερη (p>0.50) αρχίσουμε να υποθέτουμε ότι υπάρχουν πράγματι διαφορές. Πώς τυποποιούνται όλα αυτά; Τυποποιούνται αν γνωρίζουμε την κατανομή των πιθανοτήτων του πειράματός μας.
Από το σημείο αυτό, αρχίζουν τα μαθηματικά της υπόθεσης. Αυτό που πρέπει να γνωρίζετε, εν προκειμένω, είναι ότι υπάρχει τρόπος να υπολογίσουμε την πιθανότητα ένα πείραμα Bernoulli να καταλήξει σε ένα συγκεκριμένο αποτέλεσμα. Οι εξισώσεις που μας βοηθούν σε αυτό είναι, ίσως, τρομακτικές αρχικώς αλλά, όπως θα δείτε στη συνέχεια, δεν χρειάζονται ιδιαίτερα. Παρατίθενται περισσότερο για ενημερωτικούς λόγους:
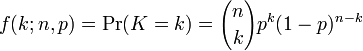
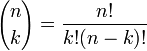
Ας υποθέσουμε ότι πραγματοποιούμε το πείραμα του νομίσματος 10 φορές, το νόμισμα είναι “τίμιο” και το αποτέλεσμα είναι να έχουμε 7 φορές “Γράμματα”. Ποια είναι η πιθανότητα να συμβεί κάτι τέτοιο; Αν αντικαταστήσετε στις παραπάνω εξισώσεις n=10 (οι φορές που πετάξαμε το νόμισμα), p=0.5 (το νόμισμα είναι τίμιο) και k=7 (είχαμε 7 φορές “Γράμματα”), το αποτέλεσμα είναι περίπου 0.12 κάτι που σημαίνει ότι αν κάνουμε όλο το πείραμα 100 φορές, μπορούμε να αναμένουμε (αλλά όχι να είμαστε βέβαιοι) ότι στις δώδεκα από αυτές θα έχουμε αυτό το αποτέλεσμα. Για όσους αρέσκονται στον τζόγο, η πιθανότητα να φέρει κανείς 10 φορές “Γράμματα” είναι 0.001, δηλαδή μια στις χίλιες.
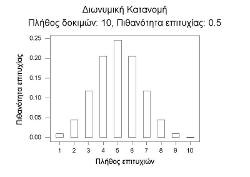
Τρέχοντας την εξίσωση αυτή για n=10 και διαφορετικές πιθανότητες (κάνοντας δηλαδή το νόμισμά μας σταδιακά όλο και πιο “βαρύ” από κάποια πλευρά) μπορούμε να σχεδιάσουμε ένα διάγραμμα που το ονομάζουμε διωνυμική κατανομή και δείχνει παραστατικά ποιες είναι οι πιθανότητες για ένα συγκεκριμένο αποτέλεσμα (επιτυχίες) με δεδομένη την πιθανότητα επιτυχίας του πειράματος γενικώς. Δείτε το διάγραμμα για p=0.5 το οποίο είναι χαρακτηριστικά συμμετρικό γύρω από το 5, κάτι που είναι λογικό: Αν το νόμισμά μας είναι τίμιο, το πιθανότερο είναι να δούμε πέντε “Γράμματα” και οι υπόλοιπες πιθανότητες είναι μικρότερες αλλά συμμετρικά μοιρασμένες μεταξύ “Γραμμάτων” και “Κορώνας”. Αν αθροίσετε το σύνολο των πιθανοτήτων επιτυχίας θα βρείτε 1. Καθώς η πιθανότητα επιτυχίας (η τιμιότητα του νομίσματος) αλλάζει προς υψηλότερες τιμές το διάγραμμα παραμορφώνεται και κινείται προς περισσότερες επιτυχίες: Είναι λογικό να αναμένουμε ότι ένα φτιαγμένο νόμισμα θα πέσει περισσότερες φορές προς την προαποφασισμένη πλευρά, επομένως και η πιθανότητα αυξάνεται, αυτό άλλωστε είναι και το νόημα μια τέτοιας κατασκευής!
 |
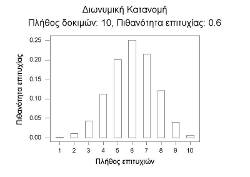 |
Διωνυμική Κατανομή για n=10 και p=0.5 |
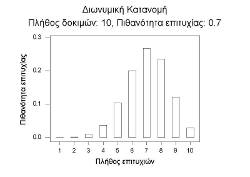
Διωνυμική Κατανομή για n=10 και p=0.6 |
 |
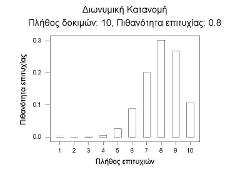 |
Διωνυμική Κατανομή για n=10 και p=0.7 |
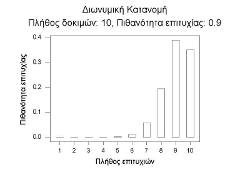
Διωνυμική Κατανομή για n=10 και p=0.8 |
 |
|
Διωνυμική Κατανομή για n=10 και p=0.9 |
Ας δούμε, τώρα, πώς όλα αυτά μεταφέρονται στον χώρο των ακροάσεων: Ήδη έχουμε δεχτεί ότι μια τυφλή δοκιμή είναι ένα πείραμα Bernoulli. Στο πείραμα αυτό γνωρίζουμε τον αριθμό των επαναλήψεων του πειράματος (το αντίστοιχο της ρίψης ενός νομίσματος), n, και το αποτέλεσμα (πόσες φορές στις n ο ακροατής βρήκε σωστά την εκδοχή). Θα θέλαμε να γνωρίζουμε αν άκουγε πράγματι διαφορές ή απλώς μάντευε στην τύχη. Στην στατιστική, αυτό μπορεί να γίνει ως εξής: Διατυπώνουμε την πρόταση “Ο ακροατής επέλεγε στην τύχη” την οποία ονομάζουμε (παραδοσιακά) Ho και προσπαθούμε να δούμε, με βάση τα αποτελέσματα πόσο πιθανό είναι να ισχύει. Για παράδειγμα, αισθανόμαστε ότι ένα πείραμα που καταλήγει σε 5/10 σωστές επιλογές δείχνει, μάλλον, τυχαίες επιλογές. Αλλά τι δείχνει το 6/10, το 7/10 ή το 67/85; Εδώ υπεισέρχεται ο στατιστικός έλεγχος της υπόθεσης Ho και όχι η αρχή της απλής πλειοψηφίας όπως, ίσως, πιστεύουν πολλοί. Για να ελέγξουμε την υπόθεσή μας, διατυπώνουμε την εναλλακτική υπόθεση Η1 η οποία δεν μπορεί παρά να είναι “Ο ακροατής δεν επέλεγε στην τύχη” και αποφασίζουμε, με βάση την διεθνή μαθηματική πρακτική, ότι θα τη δεχτούμε αν η πιθανότητα να συμβαίνει κάτι τέτοιο είναι μεγαλύτερη του 0.50. Με άλλα λόγια μπορούμε να γράψουμε: Ηο: p=0.5 H1: p>0.5 Χρησιμοποιώντας τις εξισώσεις που φαίνονται πιο πάνω μπορούμε να φτιάξουμε τον εξής πίνακα (ο οποίος αποτελεί την έκφραση με ποσοστά των διαγραμμάτων της διωνυμικής κατανομής:
| Διωνυμική κατανομή για n=10, p=0.5 και p=0.6 | ||
|---|---|---|
| Επιτυχίες (k) | Πιθανότητα (p=0.5) | Πιθανότητα (p=0.6) |
| 10 | 0.0010 | 0.0060 |
| 9 | 0.0098 | 0.0403 |
| 8 | 0.0439 | 0.1209 |
| 7 | 0.1172 | 0.2150 |
| 6 | 0.2051 | 0.2508 |
| 5 | 0.2461 | 0.2007 |
| 4 | 0.2051 | 0.1115 |
| 3 | 0.1172 | 0.0425 |
| 2 | 0.0439 | 0.0106 |
| 1 | 0.0098 | 0.0016 |
| 0 | 0.0010 | 0.0001 |
Από τον πίνακα αυτόν προκύπτει ότι αν ισχύει η Hο (p=0.5) τότε η πιθανότητα να επιτύχει ο ακροατής 8/10 σωστές αναγνωρίσεις και πάνω θα είναι: 0.0439+0.0098+0.0010=0.0547, δηλαδή κάτι παραπάνω από 5/100. Η πιθανότητα αυτή είναι πολύ μικρή αλλά όχι τόσο μικρή όσο θα θέλαμε με βάση την διεθνή πρακτική η οποία θεωρεί “απίθανο” ένα γεγονός που έχει πιθανότητας ίσες ή μικρότερες από 5%. Έτσι, απαιτούμε από τον ακροατή μας να κάνει 9 και άνω ορθές επιλογές κάτι που οδηγεί σε μια πιθανότητα 0.0098+0.0010=0.0108, δηλαδή 1%. Τώρα, πλέον μπορούμε να ισχυριστούμε ότι: “Αν ισχύει η Ho, δηλαδή αν ο ακροατής επιλέγει στην τύχη, είναι απίθανο να πετύχει 9/10 και πάνω σωστές επιλογές”, επομένως, είμαστε υποχρεωμένοι να απορρίψουμε την Ho υπέρ της εναλλακτικής πρότασης Η1 η οποία πολύ απλά δέχεται ότι ο ακροατής δεν επιλέγει στην τύχη, επομένως ακούει διαφορές! Θα μπορούσαμε, φυσικά, να αυξήσουμε το ποσοστό που θεωρούμε ως όριο απιθανότητας ας πούμε στο 20% οπότε θα επαρκούσαν 6 και άνω ορθές επιλογές (θα δούμε γιατί δεν το θέλουμε αυτό, αμέσως).
Το ποσοστό κάτω από το οποίο θεωρούμε απίθανη την τυχαία επιλογή, υπό την ισχύ της Ho και μας αναγκάζει, τελικώς, να την απορρίψουμε, το ονομάζουμε επίπεδο σημαντικότητας της δοκιμής, με άλλα λόγια, το τυπικό επίπεδο σημαντικότητας σε τέτοιες δοκιμές είναι το 0.05. Αλλά, φυσικά, μπορεί να κάνουμε και λάθος!
Υπάρχει πάντοτε η πιθανότητα ένας ακροατής να μην ακούει διαφορές (άρα να μαντεύει) και ταυτοχρόνως να είναι, απλώς, τυχερός, επειδή τίποτε δεν αποκλείει να φέρεις 9/10 και να επιλέγεις τυχαία. Τότε, θα έχουμε απορρίψει την Ho υπέρ της H1 (θα έχουμε δεχτεί ότι ακούει διαφορές) αλλά θα έχουμε κάνει λάθος. Το λάθος αυτό, της αποδοχής της H1 ενώ ισχύει η Ho, ονομάζεται Σφάλμα Τύπου Ι. Οι πιθανότητες να κάνουμε το λάθος αυτό είναι ίσες με το επίπεδο σημαντικότητας (επειδή αυτές είναι οι πιθανότητες να συμβεί το 9/10 ή περισσότερο ενώ ισχύει η Ho). Οπότε, το πείραμά μας έχει πιθανότητα 5% να καταλήξει στο λάθος συμπέρασμα ότι υπάρχουν διαφορές και είναι αυτός ο λόγος που δεν θα μας ικανοποιούσε μια επίδοση 6/10 (με επίπεδο σημαντικότητας 0.20). Οι πιθανότητας για λάθος είναι 20% και είναι απαράδεκτα μεγάλες! Σημειώστε εδώ ότι επειδή οι δυνατότητές μας είναι διακριτές (από το 8/10 πάμε αναγκαστικά στο 9/10) αντίστοιχα άλματα κάνει και το ποσοστό σφάλματος. Από κάτι περισσότερο από 5% μειώνεται, για μία μόνο πρόσθετη επιτυχία σε κάτι παραπάνω από 1%. Αυτό είναι κάτι που, επίσης, πρέπει να λαμβάνουμε υπόψιν, όταν σχεδιάζουμε την δοκιμή).
Με την ίδια λογική, μπορούμε να αποφασίσουμε να δεχτούμε την Ho, απορρίπτοντας την H1, ενώ στην πραγματικότητα η Ho δεν ισχύει, για παράδειγμα αν έχουμε p=0.6 και 9/10 κι άνω επιτυχίες. Στην περίπτωση αυτή, όπως φαίνεται στον πίνακα έχουμε επίπεδο σημαντικότητας 0.0403+0.0060=0.0463. Ποια είναι η πιθανότητα να κάνουμε λάθος; Καθορίζεται από το άθροισμα των πιθανοτήτων για 0 έως 8 ορθές επιλογές, άθροισμα το οποίο είναι 0.9537, δηλαδή ένα εξαιρετικά υψηλό ποσοστό λάθους (95%). Το σφάλμα αυτό ονομάζεται Σφάλμα Τύπου ΙΙ. To 1986, o Les Leventhal δημοσίευσε μια σχετική μελέτη με αυτήν την επισήμανση [9], η οποία έθεσε θέμα αξιοπιστίας του συγκεκριμένου στατιστικού ελέγχου, όταν ο αριθμός των πειραμάτων είναι μικρός. Η ουσία ήταν (και σωστά) ότι σε τόσο μικρά n, όσοι πρότειναν την υπόθεση H1 (δηλαδή εκείνοι που ισχυρίζονταν ότι υπάρχουν διαφορές) κινδύνευαν πολύ περισσότερο από λάθη (τύπου ΙΙ) στον στατιστικό έλεγχο, με άλλα λόγια η δοκιμή ήταν πολωμένη προς την απόρριψη της εναλλακτικής υπόθεσης! Ακολουθώντας την μαθηματική θεωρία, ο Leventhal πρότεινε δύο λύσεις, την προφανή, δηλαδή την αύξηση του n είτε με αύξηση των μουσικών κομματιών κάθε πειράματος, είτε με αύξηση των ακροατών είτε με ταυτόχρονη αύξηση και των δύο (γενικά μιλώντας, το n είναι το γινόμενο των ακροατών επί τα μουσικά κομμάτια που χρησιμοποιούνται), καθώς επίσης και έναν συμβιβασμό, με αύξηση του Σφάλματος Τύπου Ι η οποία οδηγεί σε μείωση του Σφάλματος Τύπου ΙΙ. Για κάθε n, σε ένα πείραμα, υπάρχει ένας βέλτιστος συνδυασμός σφαλμάτων. Ο συμβιβασμός έγκειται στο γεγονός ότι επιλέγοντας διαφορετικό Σφάλμα Τύπου Ι, δεν παραμένουμε στο τυπικά σωστό επίπεδο σημαντικότητας του 5%. Ο Leventhal συνόδευσε την μελέτη του με μια σειρά από πίνακες τους οποίους μπορείτε να δείτε ως αρχεία PDF εδώ:
Πίνακας 1 (n=10-25), Πίνακας 2(n=30-45), Πίνακας 3 (n=50-100), Πίνακας 4 (n=120-180).
Ας δούμε ένα παράδειγμα για την χρήση τους; Ας υποθέσουμε ότι έχουμε μια τυφλή δοκιμή με 16 επιμέρους δοκιμές (Ν ή n=16). Αυτό το 16 μπορεί να είναι ένας ακροατής με 16 κομμάτια, ή 4 ακροατές με 4 κομμάτια ή κάποιος παρόμοιος συνδυασμός. Ο πίνακας περιλαμβάνει μια στήλη με την ιδανική επίδοση (αυτήν που θεωρητικά πρέπει να πιάσει ο ακροατής ή η ομάδα) στην στήλη r, το Σφάλμα Τύπου Ι που αντιστοιχεί σε κάθε r για την απόρριψη της Ho καθώς επίσης και τα Σφάλματα Τύπου ΙΙ που αντιστοιχούν στην πραγματική επίδοση της δοκιμής. Οι λόγοι p=0.6-0.9 είναι το ποσοστό των πραγματικών επιλογών του ακροατή (στο σύνολο των δοκιμών), ή ο μέσος όρος της επίδοσης της ομάδας των ακροατών. Αν ο σχεδιαστής του πειράματος αποφασίσει να τηρήσει το επίπεδο σημαντικότητας στο 0.5%, θα απαιτήσει 12/16 επιτυχίες και άνω για να απορρίψει την Ho υπέρ της H1, επιλογή που αντιστοιχεί σε Σφάλμα Τύπου Ι ίσο με 0.0384 (η αμέσως επόμενη επιλογή, 11/16 δίνει σφάλμα μεγαλύτερο του 0.05). Αυτή η επιλογή σημαίνει ότι αν η επίδοση στη δοκιμή είναι, για παράδειγμα, 0.7 και η H1 απορριφθεί (επειδή 0.7x16=11.2<12) η πιθανότητα Σφάλματος Τύπου ΙΙ (να μην δεχτούμε ότι υπάρχουν διαφορές, ενώ -τελικώς- υπάρχουν) είναι μεγάλη και φτάνει το 0.5501, δηλαδή κοντά στο 55%. Η λύση, με βάση τον πίνακα είναι να μειώσουμε την ιδανική επίδοση στο 10/16, γεγονός που επιβάλλει Σφάλμα Τύπου Ι ίσο με 0.2272 και Σφάλμα Τύπου ΙΙ ίσο με 0.1753. Η τεχνική αυτή, αν και αυξάνει την περίπτωση να δεχτούμε λανθασμένα ότι ισχύει η H1 (κάτι για το οποίο ο Leventhal επικρίθηκε), εξισώνει τουλάχιστον τα δύο Σφάλματα. Η επιλογή που θα γίνει εδώ, είναι θέμα αυτού που σχεδιάζει την τυφλή δοκιμή.